题干本题共包含 4 个小题
简答题第1题
计算两个方案的年折旧额。
正确答案
甲方案年折旧额=30000/5=6000(元)
乙方案年折旧额=(36000-6000)÷5=6000(元)
乙方案年折旧额=(36000-6000)÷5=6000(元)
答案解析
略
简答题第2题
计算两个方案的营业现金流量。
正确答案
列表计算两个方案的营业现金流入:
营业现金流入计算表
单位:元
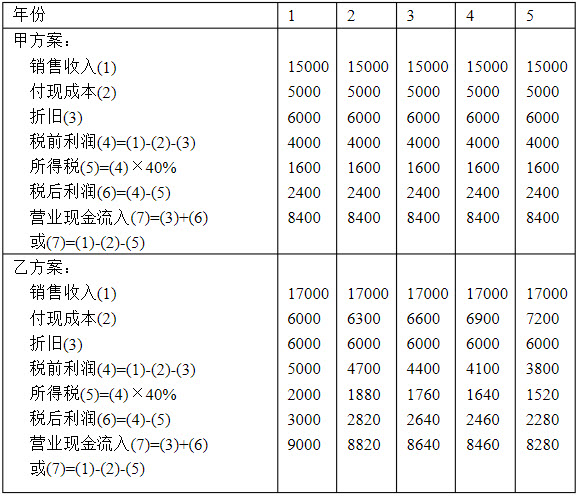
营业现金流入计算表
单位:元

答案解析
略
简答题第3题
计算两个方案的全部现金净流量。
正确答案
列表计算全部现金净流量:
全部现金净流量计算表

全部现金净流量计算表

答案解析
略
简答题第4题
计算两个方案的净现值、净现值率、获利指数、内含报酬率、投资回收期和投资报酬率。
正确答案
净现值:
甲方案净现值=8400×(P/A,10%,5)-30000=8400×3.791-30000=31844.40-30000=1844.40(元)
乙方案净现值=9000×(P/F,10%,1)+8820×(P/F,10%,2)+8640×(P/F,10%,3)+8460×(P/F,10%,4)+17280×(P/F,10%,5)-39000
=9000×0.909+8820×0.826+8640×0.751+8460×0.683+17280×0.621-39000
=38464.02-39000
=-535.98(元)
甲方案的净现值大于零,为可行方案;乙方案的净现值小于零,不可行。
净现值率:甲方案净现值率=1844.40/30000=6.148%
乙方案净现值率=-535.98/39000=-1.37%
获利指数:
甲方案现值指数=8400×(P/A,10%,5)÷30000=1.06
乙方案现值指数=38464.02÷39000=0.99
甲方案的现值指数大于1,为可行方案;乙方案现值指数小于1,不可行。
两个方案的内含报酬率:
甲方案每年现金流入量相等,可利用“年金现值系数”计算:
原始投资=每年现金流入量×年金现值系数
30000=8400×(P/A,i ,5)
(P/A,i ,5)=30000/8400=3.571
查年金现值系数表,与3.571最接近的现值系数3.605和3.433分别指向12%和14%,采用插补法确定内含报酬率为:
甲方案内含报酬率=12%+2%×[(3.605-3.571)÷(3.605-3.433)]=12.04%
乙方案各年现金流量不相等,采用“逐步测试法”:
已知i=10%,NPV=-535.98,则应降低贴现率再测试:
令i=9%,计算净现值:
NPV=9000×(P/F,9%,1)+8820×(P/F,9%,2)+8640×(P/F,9%,3)+8460×(P/F,9%,4)+17280×(P/F,9%,5)-39000 =571.20(元)
采用插值法计算:
乙方案内含报酬率=9%+1%×[(0-571.20)÷(-535.98-571.20)]=9.52%
甲方案的内含报酬率大于企业的资金成本10%,为可行方案;乙方案的内含报酬率小于资金成本,为不可行方案。
投资回收期:
甲方案各年现金流入量相等,且原始投资一次投入,可使用“公式法”计算:
甲方案回收期=30000/8400=3.57(年)
乙方案各年现金流入量不等,使用“累计法”计算:
乙方案回收期=4+(39000-9000-8820-8640-8460)÷17280=4.24(年)
进行投资决策时,回收期最短的方案为最佳。因为,投资期越短,投资风险就越小,即甲方案要优于乙方案。从这一角度看,还应将各方案的回收期与投资人要求的回收期,或基准回收期比较,只有计算出的回收期小于基准数,方案才为可行方案。
投资报酬率=年平均利润÷原始投资额
甲方案投资报酬率=4000÷30000=13.33%
乙方案投资报酬率=(5000+4700+4400+4100+3800)÷5÷39000=11.28%
(注:投资报酬率指标中,年利润或者年平均利润一般用税前利润,也可以用税后利润,只要不影响指标的相互比较就行)
甲方案净现值=8400×(P/A,10%,5)-30000=8400×3.791-30000=31844.40-30000=1844.40(元)
乙方案净现值=9000×(P/F,10%,1)+8820×(P/F,10%,2)+8640×(P/F,10%,3)+8460×(P/F,10%,4)+17280×(P/F,10%,5)-39000
=9000×0.909+8820×0.826+8640×0.751+8460×0.683+17280×0.621-39000
=38464.02-39000
=-535.98(元)
甲方案的净现值大于零,为可行方案;乙方案的净现值小于零,不可行。
净现值率:甲方案净现值率=1844.40/30000=6.148%
乙方案净现值率=-535.98/39000=-1.37%
获利指数:
甲方案现值指数=8400×(P/A,10%,5)÷30000=1.06
乙方案现值指数=38464.02÷39000=0.99
甲方案的现值指数大于1,为可行方案;乙方案现值指数小于1,不可行。
两个方案的内含报酬率:
甲方案每年现金流入量相等,可利用“年金现值系数”计算:
原始投资=每年现金流入量×年金现值系数
30000=8400×(P/A,i ,5)
(P/A,i ,5)=30000/8400=3.571
查年金现值系数表,与3.571最接近的现值系数3.605和3.433分别指向12%和14%,采用插补法确定内含报酬率为:
甲方案内含报酬率=12%+2%×[(3.605-3.571)÷(3.605-3.433)]=12.04%
乙方案各年现金流量不相等,采用“逐步测试法”:
已知i=10%,NPV=-535.98,则应降低贴现率再测试:
令i=9%,计算净现值:
NPV=9000×(P/F,9%,1)+8820×(P/F,9%,2)+8640×(P/F,9%,3)+8460×(P/F,9%,4)+17280×(P/F,9%,5)-39000 =571.20(元)
采用插值法计算:
乙方案内含报酬率=9%+1%×[(0-571.20)÷(-535.98-571.20)]=9.52%
甲方案的内含报酬率大于企业的资金成本10%,为可行方案;乙方案的内含报酬率小于资金成本,为不可行方案。
投资回收期:
甲方案各年现金流入量相等,且原始投资一次投入,可使用“公式法”计算:
甲方案回收期=30000/8400=3.57(年)
乙方案各年现金流入量不等,使用“累计法”计算:
乙方案回收期=4+(39000-9000-8820-8640-8460)÷17280=4.24(年)
进行投资决策时,回收期最短的方案为最佳。因为,投资期越短,投资风险就越小,即甲方案要优于乙方案。从这一角度看,还应将各方案的回收期与投资人要求的回收期,或基准回收期比较,只有计算出的回收期小于基准数,方案才为可行方案。
投资报酬率=年平均利润÷原始投资额
甲方案投资报酬率=4000÷30000=13.33%
乙方案投资报酬率=(5000+4700+4400+4100+3800)÷5÷39000=11.28%
(注:投资报酬率指标中,年利润或者年平均利润一般用税前利润,也可以用税后利润,只要不影响指标的相互比较就行)
答案解析
略
相似试题
某公司准备购入新设备,购置成本20万元,寿命期5年,残值2万元,新设备可使企业获得收入65万元,发生付现成本40万元,该公司资本成本率15%,所得税率25%。用NPV法决策该设备是否可以购入。
简答题查看答案
某公司每年存入银行30000元,准备三年后购入一台新设备,如果银行利率10%,试计算三年后的本利和是多少钱?
简答题查看答案
甲公司购入某上市公司发行的期限为3年债券,到期一次还本付息的债券,甲公司准备并有能力持有至到期,甲公司应将该项投资划分为()。
单选题查看答案
境内某企业从境外公司购入大型设备一套,并约定境外公司在设备到位后须技术人员若干名到境内企业进行调试和安装,该技术人员来华的薪金由境内企业负担。则该笔薪金在以下两周可能的情况下应如何办理申报?
简答题查看答案
宏大公司原有一套生产设备是4年前购入的,原购置成本200000元,估计尚可使用6年,假定期满无残值,按直线法已提取折旧80000元。使用该机器每年可获销售收入298000元,每年付现成本226000元。 该公司为提高产量和质量,准备购置一台新设备,约需价款300000元,估计可使用6年,期满有残值15000元。构入新机器时旧机器可作价90000元。使用新机器后每年可增加销售收入50000元,同时每年节约付现成本20000元。所得税率为33%。请计算有关指标: (1)新旧设备原始投资差额; (2)新旧设备每年折旧差额; (3)新旧设备每年净利润差额; (4)新旧设备营业现金流量差额; (5)新旧设备的残值差额。
简答题查看答案