简答题
正确答案
以“认识长方形的对边相等”为内容，设计一个教学片断。
将教学过程设计成四个层次：
①让学生说一说：我们周围有哪些长方形物体？学生会举出黑板、桌面、教室的门、课本的封面等例子。
②要求学生仔细观察：看一看、想一想，这些长方形的四条边的长短有什么关系？学生经过观察后，会猜想：长方形相对的两条边长度相等。
③教师进一步提出问题：同学们敢于大胆猜想的精神值得鼓励！我们怎样才能验证长方形相对的两条边的长短相等呢？这时，学生会想出许多办法，如：用尺量、将图形对折等方法。教师顺势引导学生通过量量、折折的具体操作，确信长方形相对的两条边长短相等。教师板书：长方形对边相等。接着，师生讨论长方形“对边”的含义，以及一个长方形有几组对边的问题。
④巩固长方形对边相等的认识。利用多媒体展示下面的长方形：
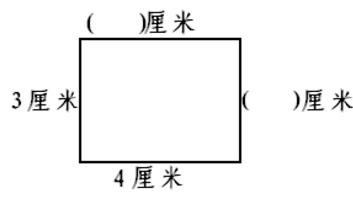
教师提问：如何填写括号内的数字？为什么？
要求学生会用“因为…所以…”句式回答。如“因为长方形的对边相等，已知长方形的一条边是3厘米，所以它的对边也是3厘米。”
将教学过程设计成四个层次：
①让学生说一说：我们周围有哪些长方形物体？学生会举出黑板、桌面、教室的门、课本的封面等例子。
②要求学生仔细观察：看一看、想一想，这些长方形的四条边的长短有什么关系？学生经过观察后，会猜想：长方形相对的两条边长度相等。
③教师进一步提出问题：同学们敢于大胆猜想的精神值得鼓励！我们怎样才能验证长方形相对的两条边的长短相等呢？这时，学生会想出许多办法，如：用尺量、将图形对折等方法。教师顺势引导学生通过量量、折折的具体操作，确信长方形相对的两条边长短相等。教师板书：长方形对边相等。接着，师生讨论长方形“对边”的含义，以及一个长方形有几组对边的问题。
④巩固长方形对边相等的认识。利用多媒体展示下面的长方形：
教师提问：如何填写括号内的数字？为什么？
要求学生会用“因为…所以…”句式回答。如“因为长方形的对边相等，已知长方形的一条边是3厘米，所以它的对边也是3厘米。”
答案解析
略
相似试题
假定学生已有了除法商的不变性知识经验，在学习分数的性质时，请你设计一个孕育“类比法”教学片断。
简答题查看答案
人们运用归纳法，得出对一类现象的某种一般性认识的一种推测性的判断，即猜想，这种思想方法称为（）
单选题查看答案
人们运用类比法，根据一类事物所具有的某种属性，得出与其类似的事物也具有这种属性的一种推测性的判断，即猜想，这种思想方法称为（）
单选题查看答案
猜想就是根据事物的现象，对其本质属性进行（）或者是根据一类事物中的个别事物的属性对该类事物的共同属性进行（）这样的思维方法叫做猜想。
填空题查看答案
试比较归纳猜想与类比猜想的异同。
简答题查看答案
归纳猜想的思维步骤为（）
单选题查看答案
初等数学都是以（）为其研究对象，运用这些知识可以有效地描述和解释相对稳定的事物和现象，对于运动变化的事物和现象，它们显然无能为力。
单选题查看答案
为避免数学以后再出现类似问题，数学家对集合论的严格性以及数学中的概念构成法和数学论证方法进行逻辑上、哲学上的思考，其目的是力图为整个数学奠定一个坚实的基础。随着对数学基础的深入研究，在数学界产生了数学基础研究的三大学派（）
单选题查看答案
数学分类有现象分类和本质分类的区别。所谓现象分类，是指仅仅根据数学对象的（）进行分类。
单选题查看答案