某县要了解该县小学六年级学生语文理解程度是否达到及格水平(60分)。为此,从全体六年级学生中用简单随机放还抽样方法抽取了400人进行测试,得到平均成绩61.6分,标准差14.4分。要根据样本数据对总体参数的论断值(语文理解程度的期望值60分)作显著性检验,显著水平先后按α=0.05和α=0.01考虑。请就上面的工作任务回答下列问题:
题干本题共包含 9 个小题
简答题第1题
指出由样本数据观测到何种差异?
正确答案
由样本数据观察到的差异:
样本平均数61.6分,不同于对总体平均值的猜想(60分)。
样本平均数61.6分,不同于对总体平均值的猜想(60分)。
答案解析
略
简答题第2题
指出出现这种差异的两种可能的原因是什么?
正确答案
出现这种差异的两种可能的原因:
第一种可能:总体平均值的确为60分,样本平均数与60分的差异纯属于抽样所产生的机会变异。
第二种可能:总体平均值不是60分,样本平均数与60分的差异反映了总体平均值不同于60分的这种真实存在的差异。
第一种可能:总体平均值的确为60分,样本平均数与60分的差异纯属于抽样所产生的机会变异。
第二种可能:总体平均值不是60分,样本平均数与60分的差异反映了总体平均值不同于60分的这种真实存在的差异。
答案解析
略
简答题第3题
针对这两种可能的原因提出相应的两种假设(原假设和备择假设),指出所提出的假设对应着单侧检验还是双侧检验,说明为什么要用单侧检验或者双侧检验?
正确答案
建立假设
①若想了解学生的语文理解程度是否为60分(后来通知学生改为这样写)

上述一组假设对应着双尾检验。
用双尾检验的理由是:我们所关心的仅仅是,μ是否等于60(将μ=60设为原假设)。若检验统计量的样本值落在检验统计量的概率分布曲线的左尾部(这意味着μ<60)或右尾部(这意味着μ>60),都属于我们所关心的情况的对立情况,都需要拒绝原假设。因而要把拒绝域同时放在左、右两个尾部,即,进行双尾检验。
②若想了解学生的语文理解程度是否达到或超过60分(教材中原来只写“是否达到”,在理解上容易产生歧义,应加上“或超过”)

上述一组假设对应着左单尾检验。
用左单尾检验的理由是:我们所关心的是,μ是否大于或等于60(将μ≥60设为原假设)。若检验统计量的样本值落在检验统计量的概率分布曲线的左尾部(这意味着μ<60),这属于我们所关心的情况的对立情况,需要拒绝原假设;至于检验统计量的样本值落在右尾部(这意味着μ>60)时,这属于我们所关心的情况,不需要拒绝原假设。因而只把拒绝域放在左尾部,即,进行左单尾检验。
①若想了解学生的语文理解程度是否为60分(后来通知学生改为这样写)

上述一组假设对应着双尾检验。
用双尾检验的理由是:我们所关心的仅仅是,μ是否等于60(将μ=60设为原假设)。若检验统计量的样本值落在检验统计量的概率分布曲线的左尾部(这意味着μ<60)或右尾部(这意味着μ>60),都属于我们所关心的情况的对立情况,都需要拒绝原假设。因而要把拒绝域同时放在左、右两个尾部,即,进行双尾检验。
②若想了解学生的语文理解程度是否达到或超过60分(教材中原来只写“是否达到”,在理解上容易产生歧义,应加上“或超过”)

上述一组假设对应着左单尾检验。
用左单尾检验的理由是:我们所关心的是,μ是否大于或等于60(将μ≥60设为原假设)。若检验统计量的样本值落在检验统计量的概率分布曲线的左尾部(这意味着μ<60),这属于我们所关心的情况的对立情况,需要拒绝原假设;至于检验统计量的样本值落在右尾部(这意味着μ>60)时,这属于我们所关心的情况,不需要拒绝原假设。因而只把拒绝域放在左尾部,即,进行左单尾检验。
答案解析
略
简答题第4题
仿照式(6.7)构造检验统计量(如在那里说明过的:这个检验统计量服从t分布。不过,由于我们在这里所使用的是一个400人的足够大的样本,因而可以用标准正态分布作为t分布的近似)。
正确答案
构造检验统计量:
在原假设H0:μ=60成立的条件下,有下列检验统计量服从自由度为n–1=400–1的t分布。由于自由度相当大,故这个分布同标准正态分布非常接近。
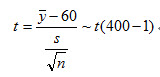
在原假设H0:μ=60成立的条件下,有下列检验统计量服从自由度为n–1=400–1的t分布。由于自由度相当大,故这个分布同标准正态分布非常接近。
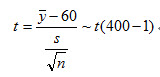
答案解析
略
简答题第5题
计算检验统计量的样本值。
正确答案
计算检验统计量的样本值:
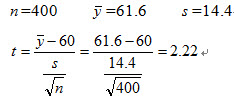
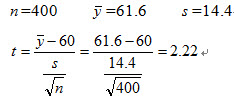
答案解析
略
简答题第6题
根据上述样本值查表确定观测到的显著性水平。
正确答案
观察到的显著水平(P值)
查标准正态分布表,z=2.22时阴影面积值为0.4868。故:
右尾P值=P(2.22左尾P值=P(2.22>z>–∞)=0.5+0.4868=0.9868
查标准正态分布表,z=2.22时阴影面积值为0.4868。故:
右尾P值=P(2.22
答案解析
略
简答题第7题
用观测到的显著性水平与检验所用的显著性水平标准比较(注意:如果是单侧检验,这个标准用α值,如果是双侧检验,这个标准用α/2值),并说明,通过比较,你是否认为得到了足以反对“观测到的差异纯属机会变异”这一论断(或是足以反对原假设)的足够的证据?为什么?
正确答案
用P值检验规则做检验
①学生的语文理解程度是否为60分(H0:μ=60;H1:μ≠60)——双尾检验
ⅰ)若规定α=0.05
检验用的显著水平标准为α/2=0.05/2=0.025
由于右尾P值=0.0132<0.025,故拒绝原假设。
ⅱ)若规定α=0.01
检验用的显著水平标准为α/2=0.01/2=0.005
由于右尾P值=0.0132>0.025,故不能拒绝原假设。
②学生的语文理解程度是否达到或超过60分(H0:μ≥60;H1:μ<60)——左单尾检验
ⅰ)若规定α=0.05
检验用的显著水平标准为α=0.05
由于左尾P值=0.9868>0.05,故不能拒绝原假设。
ⅱ)若规定α=0.01
检验用的显著水平标准为α=0.01
由于左尾P值=0.9868>0.01,故不能拒绝原假设。
①学生的语文理解程度是否为60分(H0:μ=60;H1:μ≠60)——双尾检验
ⅰ)若规定α=0.05
检验用的显著水平标准为α/2=0.05/2=0.025
由于右尾P值=0.0132<0.025,故拒绝原假设。
ⅱ)若规定α=0.01
检验用的显著水平标准为α/2=0.01/2=0.005
由于右尾P值=0.0132>0.025,故不能拒绝原假设。
②学生的语文理解程度是否达到或超过60分(H0:μ≥60;H1:μ<60)——左单尾检验
ⅰ)若规定α=0.05
检验用的显著水平标准为α=0.05
由于左尾P值=0.9868>0.05,故不能拒绝原假设。
ⅱ)若规定α=0.01
检验用的显著水平标准为α=0.01
由于左尾P值=0.9868>0.01,故不能拒绝原假设。
答案解析
略
简答题第8题
根据提出的显著性水平建立检验规则,然后用检验统计量的样本值与检验规则比较,重新回答上条的问题。
正确答案
用临界值值检验规则做检验
①学生的语文理解程度是否为60分(H0:μ=60;H1:μ≠60)——双尾检验
ⅰ)若规定α=0.05
查标准正态分布表,zα/2=z0.05/2=z0.025=1.96,故,拒绝域为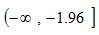 和
和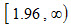 ,接受域为
,接受域为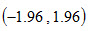 。
。
由于z=2.22>1.96,检验统计量的样本值落在拒绝域,故拒绝原假设。
ⅱ)若规定=0.01
查标准正态分布表,zα/2=z0.01/2=z0.005=2.575,故,拒绝域为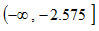 和
和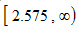 ,接受域为
,接受域为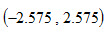 。
。
由于z=2.22<2.575,检验统计量的样本值落在接受域,故不能拒绝原假设。
②学生的语文理解程度是否达到或超过60分(H0:μ≥60;H1:μ<60)——左单尾检验
ⅰ)若规定α=0.05
查标准正态分布表,在左尾部有zα=z0.05=–1.645,故,拒绝域为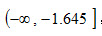 ,接受域为
,接受域为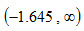 。
。
由于z=2.22>–1.645,检验统计量的样本值落在接受域,故不能拒绝原假设。
ⅱ)若规定α=0.01
查标准正态分布表,在左尾部有zα=z0.01=–2.325,故,拒绝域为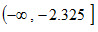 ,接受域为
,接受域为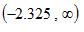 。
。
由于z=2.22>–2.325,检验统计量的样本值落在接受域,故不能拒绝原假设。
①学生的语文理解程度是否为60分(H0:μ=60;H1:μ≠60)——双尾检验
ⅰ)若规定α=0.05
查标准正态分布表,zα/2=z0.05/2=z0.025=1.96,故,拒绝域为
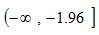 和
和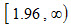 ,接受域为
,接受域为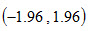 。
。由于z=2.22>1.96,检验统计量的样本值落在拒绝域,故拒绝原假设。
ⅱ)若规定=0.01
查标准正态分布表,zα/2=z0.01/2=z0.005=2.575,故,拒绝域为
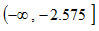 和
和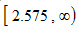 ,接受域为
,接受域为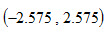 。
。由于z=2.22<2.575,检验统计量的样本值落在接受域,故不能拒绝原假设。
②学生的语文理解程度是否达到或超过60分(H0:μ≥60;H1:μ<60)——左单尾检验
ⅰ)若规定α=0.05
查标准正态分布表,在左尾部有zα=z0.05=–1.645,故,拒绝域为
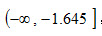 ,接受域为
,接受域为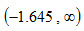 。
。由于z=2.22>–1.645,检验统计量的样本值落在接受域,故不能拒绝原假设。
ⅱ)若规定α=0.01
查标准正态分布表,在左尾部有zα=z0.01=–2.325,故,拒绝域为
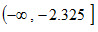 ,接受域为
,接受域为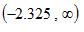 。
。由于z=2.22>–2.325,检验统计量的样本值落在接受域,故不能拒绝原假设。
答案解析
略
简答题第9题
根据上面所做的工作,针对本题的研究任务给出结论性的表述。
正确答案
检验结论
①学生的语文理解程度是否为60分
ⅰ)若规定α=0.05
样本数据显著地表明,学生的语文理解程度并非恰好为60分。上述结论的双尾显著水平为0.05。
ⅱ)若规定α=0.01
样本数据提供的证据不足以推翻学生的语文理解程度恰好为60分的假设,也就是说,学生的语文理解程度有可能恰好为60分。上述结论的双尾显著水平为0.01。
②学生的语文理解程度是否达到或超过60分
ⅰ)若规定α=0.05
样本数据提供的证据几乎完全没有理由推翻学生的语文理解程度达到或超过60分的假设,也就是说,可以认为学生的语文理解程度达到或超过了60分。上述结论的单尾显著水平为0.05。
ⅱ)若规定α=0.01
样本数据提供的证据几乎完全没有理由推翻学生的语文理解程度达到或超过60分的假设,也就是说,可以认为学生的语文理解程度达到或超过了60分。上述结论的单尾显著水平为0.01。
①学生的语文理解程度是否为60分
ⅰ)若规定α=0.05
样本数据显著地表明,学生的语文理解程度并非恰好为60分。上述结论的双尾显著水平为0.05。
ⅱ)若规定α=0.01
样本数据提供的证据不足以推翻学生的语文理解程度恰好为60分的假设,也就是说,学生的语文理解程度有可能恰好为60分。上述结论的双尾显著水平为0.01。
②学生的语文理解程度是否达到或超过60分
ⅰ)若规定α=0.05
样本数据提供的证据几乎完全没有理由推翻学生的语文理解程度达到或超过60分的假设,也就是说,可以认为学生的语文理解程度达到或超过了60分。上述结论的单尾显著水平为0.05。
ⅱ)若规定α=0.01
样本数据提供的证据几乎完全没有理由推翻学生的语文理解程度达到或超过60分的假设,也就是说,可以认为学生的语文理解程度达到或超过了60分。上述结论的单尾显著水平为0.01。
答案解析
略