单选题
计算
A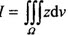
B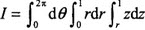
C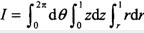
D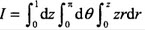
正确答案
答案解析
略
相似试题
球面x2+y2+z2=14在点(1,2,3)处的切平面方程是().
单选题查看答案
设Ω为曲面x2+y2=2z及平面z=2所围成的空间闭区域,则三重积分的值是().
单选题查看答案
设L为抛物线y=x2上从0(0,0)到P(1,1)的一段弧,则曲线积分的值是().
单选题查看答案
设D={(x,y)|x2+y2≤y,x≥0},则二重积分 化为极坐标下的累次积分为().
单选题查看答案
D域由x轴,x2+y2-2x=0(y≥0)及x+y=2所围成,f(x,y)是连续函数,转化为二次积分为()。
单选题查看答案
由曲线y=3-x2与直线y=2x所围成的图形的面积是().
单选题查看答案
方程(x2+y)dx+(x-2y)dy=0的通解是().
单选题查看答案
设D是曲线y=x2与y=1所围闭区域,等于()。
单选题查看答案
设D={(x,y)|1≤x2+y2≤4},则二重积分的值是().
单选题查看答案
 ,其中Ω为z2=x2+y2,z=1所围成的立体,则正确的解法是()。
,其中Ω为z2=x2+y2,z=1所围成的立体,则正确的解法是()。