单选题
以2丌为周期的函数f（x）在[-π，π）上的表达式为f（x）=
，f（x）的傅里叶级数在x=π处收敛于（）。A0
Bπ
C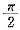
D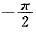
正确答案
答案解析
由狄利克雷充分条件，它收敛于
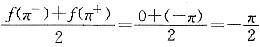，故选（D）。
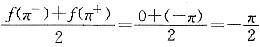，故选（D）。 相似试题
设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是奇函数时，下面结论正确的是（）。
单选题查看答案
设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是偶函数时，下面结论正确的是（）。
单选题查看答案
设随机变量X的密度函数为f（x）=Ae-|x|，-∞＜x＜+∞，F（x）是X的分布函数，则有（）。
单选题查看答案
若函数f（x）=（cos3x）/3-acosx在x=π/6处取得极值，则a的值为（）
单选题查看答案
设连续型随机变量X的分布函数，密度函数为f（x），则f（x）=（）。
单选题查看答案
设X的密度函数为f（x）=Ae-|x|，则系数A=（）。
单选题查看答案
设随机变量X的分布函数为F（x），则下列结论正确的是（）。
单选题查看答案
设F（x），G（x）是f（x）的两个原函数，则下面的结论不正确的是（）。
单选题查看答案
设F（x）是随机变量X的分布函数，则下列说法不正确的是（）。
单选题查看答案