简答题
正确答案
1、CVaR模型(Condition Value at Risk):
条件风险价值(CVaR)模型是指在正常市场条件下和一定的置信水平α上,测算出在给定的时间段内损失超过VaRa的条件期望值。
设X是描述证券组合损失的随机变量,F(x)是其概率分布函数,则条件风险价值可以表示为:
CVaR模型在一定程度上克服了VaR模型的缺点不仅考虑了超过VaR值的频率,而且考虑了超过VaR值损失的条件期望,有效的改善了VaR模型在处理损失分布的后尾现象时存在的问题。当证券组合损失的密度函数是连续函数时,CVaR模型是一个一致性风险度量模型,具有次可加性,但当证券组合损失的密度函数不是连续函数时,CVaR模型不再是一致性风险度量模型,即CVaR模型不是广义的一致性风险度量模型,需要进行一定的改进。
2、ES模型(Expect shortfall):
期望损失ES是2001年由Acerbi引进的、近年来受到银行界关注、并且得到采用的一种风险度量方法。该模型是在CVaR基础上的改进版,它是一致性风险度量模型。如果损失X的密度函数是连续的,则ES模型的结果与CVaR模型的结果相同,如果损失X的密度函数是不连续的,则两个模型计算出来的结果有一定差异,定义为:
设X是描述证券组合损失的随机变量,是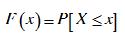 其概率分布函数,令
其概率分布函数,令
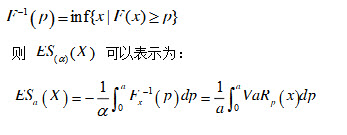
ES模型对于损失X的分布没有特殊的要求,在分布函数连续和不连续的情况下都能保持一致性风险度量这一性质,使该模型不仅可以应用到任何的金融工具的风险度量和风险控制,也可以处理具有任何分布形式的风险源,而且保证了在给定风险量的约束条件下最大化预期收益组合的唯一性。例如对两个债券,我们采用ES模型度量债券A和B,以及组合A+B的风险指标,如下表:

可以看到债券A和B风险的和大于组合A+B,与分散性投资理论相一致。但是,ES也存在缺陷,它与二阶随机占有不相容。举例如下:设x、y为两个风险,分布函数分别为:

即y为离散型的随机变量,分别以概率0.011、0.039、0.95取值-99.9、-84和10;x为连续型随机变量和离散型随机变量的混合,分别以0.05的概率在区间【-90,-85】上取值(为其上的均值分布)、以概率0.95取值10。
条件风险价值(CVaR)模型是指在正常市场条件下和一定的置信水平α上,测算出在给定的时间段内损失超过VaRa的条件期望值。
设X是描述证券组合损失的随机变量,F(x)是其概率分布函数,则条件风险价值可以表示为:

CVaR模型在一定程度上克服了VaR模型的缺点不仅考虑了超过VaR值的频率,而且考虑了超过VaR值损失的条件期望,有效的改善了VaR模型在处理损失分布的后尾现象时存在的问题。当证券组合损失的密度函数是连续函数时,CVaR模型是一个一致性风险度量模型,具有次可加性,但当证券组合损失的密度函数不是连续函数时,CVaR模型不再是一致性风险度量模型,即CVaR模型不是广义的一致性风险度量模型,需要进行一定的改进。
2、ES模型(Expect shortfall):
期望损失ES是2001年由Acerbi引进的、近年来受到银行界关注、并且得到采用的一种风险度量方法。该模型是在CVaR基础上的改进版,它是一致性风险度量模型。如果损失X的密度函数是连续的,则ES模型的结果与CVaR模型的结果相同,如果损失X的密度函数是不连续的,则两个模型计算出来的结果有一定差异,定义为:
设X是描述证券组合损失的随机变量,是
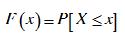 其概率分布函数,令
其概率分布函数,令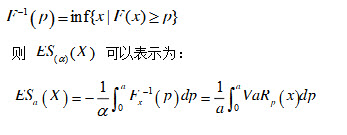
ES模型对于损失X的分布没有特殊的要求,在分布函数连续和不连续的情况下都能保持一致性风险度量这一性质,使该模型不仅可以应用到任何的金融工具的风险度量和风险控制,也可以处理具有任何分布形式的风险源,而且保证了在给定风险量的约束条件下最大化预期收益组合的唯一性。例如对两个债券,我们采用ES模型度量债券A和B,以及组合A+B的风险指标,如下表:

可以看到债券A和B风险的和大于组合A+B,与分散性投资理论相一致。但是,ES也存在缺陷,它与二阶随机占有不相容。举例如下:设x、y为两个风险,分布函数分别为:

即y为离散型的随机变量,分别以概率0.011、0.039、0.95取值-99.9、-84和10;x为连续型随机变量和离散型随机变量的混合,分别以0.05的概率在区间【-90,-85】上取值(为其上的均值分布)、以概率0.95取值10。
答案解析
略
相似试题
风险是如何刻画的?请给出两种降低风险的方法,并举例说明。
简答题查看答案
给出技术这一概念的定义并举例说明。
简答题查看答案
比较缓冲区分析和叠置分析的概念,并举例说明这两种空间分析方法的用途。
简答题查看答案
信息系统类型的划分方法有哪两种?试举例说明。
简答题查看答案
度量生产能力的形式有哪几种?请举例说明。
简答题查看答案
举出在市场营销中常用的几种经营策略(不少于5种)并解释(或举例说明)其中任意两种。
简答题查看答案
基于概率的信息度量,是()在研究信息的通信理论时给出的信息度量方法。
单选题查看答案
解释修正成本的含义,并举例说明其成本处理方法。
简答题查看答案
估算软件项目的工作量的方法有哪些,并举例说明。
简答题查看答案