单选题
A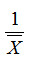
B
C
D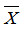
正确答案
答案解析
略
相似试题
雷达的圆形屏幕半径为R,设目标出现点(X,Y)在屏幕上服从均匀分布. (1)求P{Y>0|Y>X}; (2)设M=max{X,Y},求P{M>0}.
简答题查看答案
设X与Y是两个相互独立的随机变量,X在[0,1]上服从均匀分布,Y的概率密度为 (1)求(X,Y)的联合概率密度,(2)求概率P(Y≥X)。
简答题查看答案
设总体X服从几何分布:求p的极大似然估计量。
简答题查看答案
设X在区间[a,b]上服从均匀分布,则数学期望EX=()
单选题查看答案
设随机变量X与Y相互独立,且均服从区间[0,3]上的均匀分布,求P{max{X,Y}≤1}.
简答题查看答案
设X服从均匀分别U[2,4],Y服从指数分布e(2),且X与Y相互独立。 求(1)(X,Y)的联合概率密度; (2)E(2X+4Y); (3)D(X-2Y)。
简答题查看答案
设X在区间[a,b]上服从均匀分布,则方差DX=a+b
判断题查看答案
设随机变量X在(0,1)上服从均匀分布求Y=-2lnX的概率密度。
简答题查看答案
设随机变量X服从参数为2的指数分布.证明:Y=1 e 2X在区间(0,1)上服从均匀分布.
简答题查看答案