简答题
正确答案
(1)弄清实际问题加以化简。
经分析,为了建立旅馆一天收入的数学模型,可作如下假设:
①设每间客房的最高定价为160元;
②根据题中提供的数据,设随着房价的下降,住房率呈线性增长;
③设旅馆每间客房定价相等。
(2)建立数学模型。
根据题意,设y表示旅馆一天的总收入,x为与160元相比降低的房价。
由假设②,可得每降低1元房价,住房率增加为 10%/20=0.005因此一天的总收入为y=150(160-x(0.55+0.005x))
由于0.55=0.005x≦1,可知0≦x≦90.
于是问题归结为:当0≦x≦90时,求y的最大值点,即求解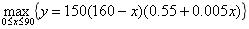
(3)模型求解。
将左边除以(150×0.005)得y’=-x2+50x+17600
由于常数因子对求最大值没有影响,因此可化为y’求的最大值点。利用配方法得y’=-(x-25)2+18225
已知当x=25时y’最大,因此可知最大收入对应的住房定价为160元-25元=135元
相应的住房率为0.55+0.005×25=67.5%最大收入为150×135×67.5%=13668.75(元)
(4)检验。
容易验证此收入在已知各种客房定价的对应收入中确实是最大的,这可从下面表格中看出。
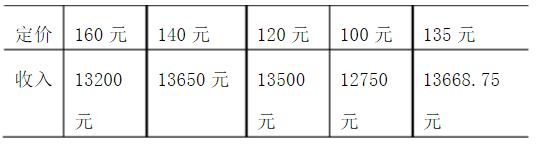
如果每间客房定价为180元,住房率为45%,其相应收入只有12150元。由此可见假设①是合理的。实际上二次函数在[0,90]之内只有一个极值点。
经分析,为了建立旅馆一天收入的数学模型,可作如下假设:
①设每间客房的最高定价为160元;
②根据题中提供的数据,设随着房价的下降,住房率呈线性增长;
③设旅馆每间客房定价相等。
(2)建立数学模型。
根据题意,设y表示旅馆一天的总收入,x为与160元相比降低的房价。
由假设②,可得每降低1元房价,住房率增加为 10%/20=0.005因此一天的总收入为y=150(160-x(0.55+0.005x))
由于0.55=0.005x≦1,可知0≦x≦90.
于是问题归结为:当0≦x≦90时,求y的最大值点,即求解
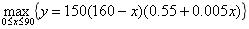
(3)模型求解。
将左边除以(150×0.005)得y’=-x2+50x+17600
由于常数因子对求最大值没有影响,因此可化为y’求的最大值点。利用配方法得y’=-(x-25)2+18225
已知当x=25时y’最大,因此可知最大收入对应的住房定价为160元-25元=135元
相应的住房率为0.55+0.005×25=67.5%最大收入为150×135×67.5%=13668.75(元)
(4)检验。
容易验证此收入在已知各种客房定价的对应收入中确实是最大的,这可从下面表格中看出。

如果每间客房定价为180元,住房率为45%,其相应收入只有12150元。由此可见假设①是合理的。实际上二次函数在[0,90]之内只有一个极值点。
答案解析
略
相似试题
鸽笼原理可叙述为:若n+1只鸽子飞进n个笼子里,则至少有一个笼子里至少飞进()只鸽子。
单选题查看答案
简述《国家数学课程标准》的几个主要特点。
简答题查看答案
数学思想方法,是指现实世界的()反映到人们的意识之中,经过()而产生的结果。数学思想方法是对数学事实和理论经过概括后产生的本质认识。
填空题查看答案
设计运用“猜想”进行数学教学的一个片断。
简答题查看答案
特殊化的作用在于,当研究的对象比较复杂时,通过研究对象的特殊情况,能使我们对研究对象有个初步了,且它的作用还在于,事物的()存在于()之中。
填空题查看答案
在反例反驳中,构造一个反例必须满足条件:()、()
填空题查看答案
算法是由一组()组成的一个过程。一个算法实质上就是解决一类问题的一个处方。
单选题查看答案
例如,“菱形→等边四边形→平行四边形→四边形”这是一个()过程。
单选题查看答案
例如,“等腰直角三角形→等腰三角形→直角三角形→ 三角形”这是一个()过程。
单选题查看答案